CodingKaro

4.7

3K+ Downloads

One of its unique features is an automated coding contest reminder, which sets alarms for upcoming coding contests on popular platforms like CodeChef, CodeForces, and LeetCode, without the need for user input. This feature ensures that users never miss a coding contest and can stay updated with the latest coding challenges.

CodingKaro

4.7

3K+ Downloads

Latest Posts

Number of subsequences in a string divisible by N | Interview Question | Find count of subsequences which are divisible by 4.

raunit- inCoding

Given a large number as string (size upto 10^5). Find count of subsequences which are divisible by 4 ( asked in salesforce ). Find count of subsequences which are divisible by N.

Build an Email Tracker App with Flask & Telegram | Get Instant Email Read Notifications on Telegram

raunit- inOthers

Create an email tracker app using Flask to send read notifications to Telegram. Learn Base64 decoding, IP-based location tracking, and how to deploy with Docker effortlessly.

What is Get Link : Connecting You? What are the advantages of Get Link? Features and Usage

raunit- inOthers

GetLink connects you with ease. Learn about its key advantages, features, and practical usage tips to enhance your experience.

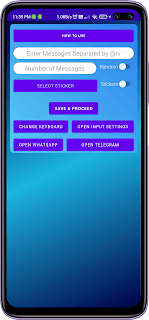
WhatsApp Bomber - Unlimited Message | Prank with Friends

raunit- inOthers

Bombard your friends with endless WhatsApp messages and have the last laugh with the new WhatsApp Bomber app! This clever tool lets you send unlimited messages with just a single click.

Getting All Cookies From A Website Using Developer Console

raunit- inOthers

Learn to retrieve all cookies from a website effortlessly with the Developer Console. Follow our comprehensive guide for clear, actionable steps and tips.

89. Gray Code - LeetCode Solution | C++ | Go | Kotlin | Java | JS | TS | Python

raunit- inLeetcode

Explore the Gray Code problem on LeetCode with comprehensive solutions and explanations in various programming languages. Perfect for coding enthusiasts!

Fixing java.lang.OutOfMemoryError: Java heap space | Android Studio Error

raunit- inAndroid

Learn how to fix the "java.lang.OutOfMemoryError: Java heap space" error in Android Studio. Follow our expert tips to improve your development efficiency.

DBMS Notes by CodeHelp | Love Babbar DBMS Notes Download

raunit- inNotes

Love Babbar DBMS Notes - Free DBMS Tutorials | Love Babbar

Complete Operating System for InterViews | OS by Love Babbar PDF

raunit- inNotes

Love Babbar OS Tutorials - Free | Inside Look at Love Babbar's Operating System PDF: Everything You Need to Know